Blended Learning Design

Data Literacy through Sports Analytics

Tina Leard (Cybera)
Michael Lamoureux (University of Calgary)

October 2020

Content and context

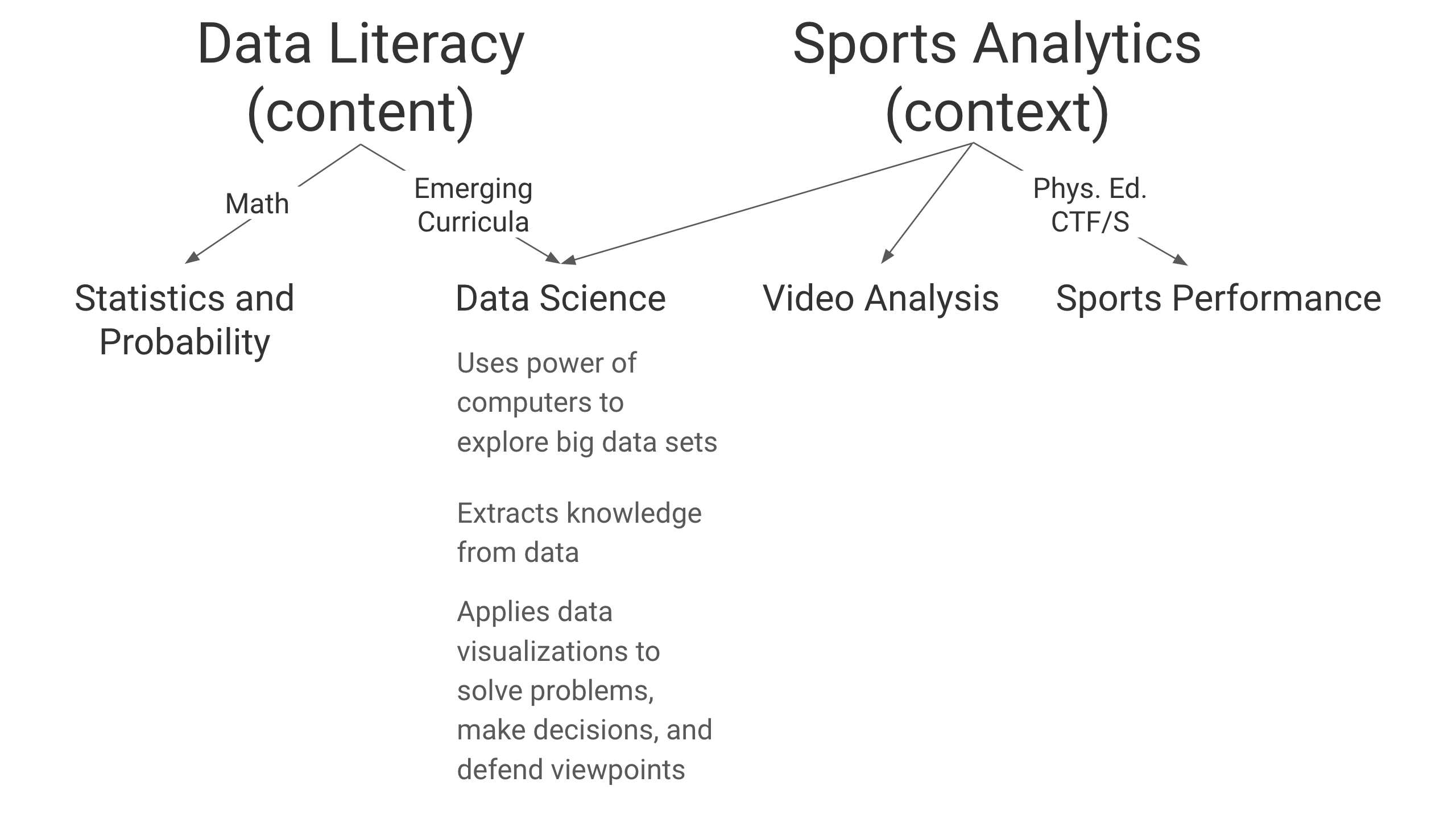
(Alberta Education, 2000, 2007, updated 2016, 2017)

Bridging expert to novice

Data visualization learning progression

Data visualization learning progression

Data gathering learning progression

Source: Pervasive and Persistent Understandings about Data,
Kastens (2014)

Authentic learning approach

• Learning design based on interdisciplinary
  

connections and real-world examples

• Industry-aligned data science analysis process
• Python, an all-purpose programming language
• Jupyter notebook, a free industry-standard tool for data scientists
• CallystoHub, free cloud computing

Learning design and athlete development

U15 training to train

• Promotes tactical strategies for in-game decision making, reading the situation and inferring
• Focuses on the team and the process
• Situates personal goals within a team approach

U18 training to compete

• Focuses more on individual strategies and goals

Learning design and U18 sports analytics

Online communication,
sometimes through shared video analysis spaces

Video replay during games and training

Post–game video analysis, limitted statistics

Learning design and flexibility

Analyzing youth field hockey data to make decisions

Learning design and context notes

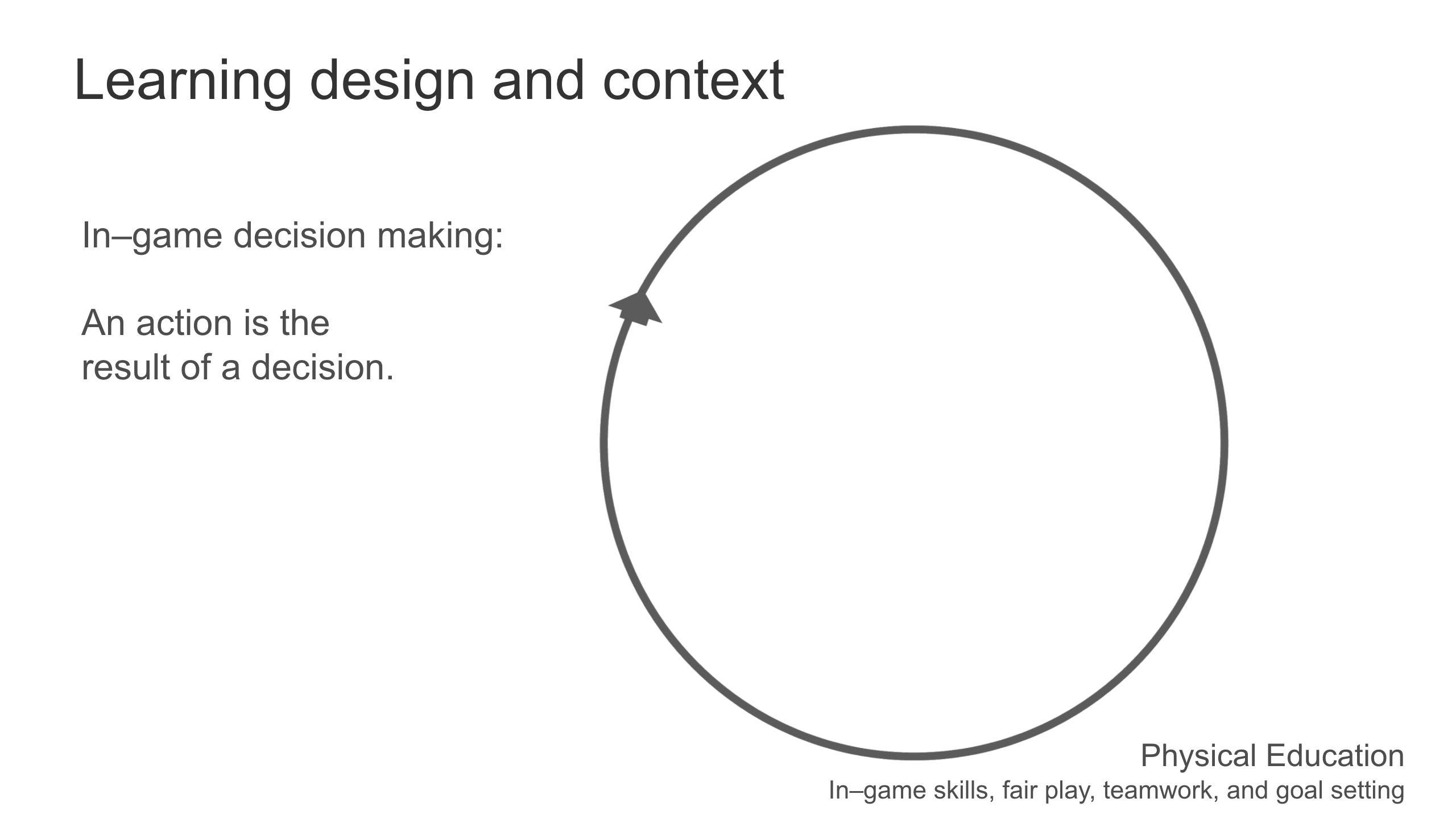
The context is physical education, and the content is statistics. Within physical education, in-game skills, fair play, teamwork, and goal setting are integrated. Those outcomes can be applied to in-game decision making. The goal setting can also be part of the communication resulting from the data analysis. When considering in-game decision making, we can define an action as the result of a decision. Decision making is part of a learning cycle that incorporates a technological feedback loop.

(Alberta Education, 2000)

Learning cycle notes

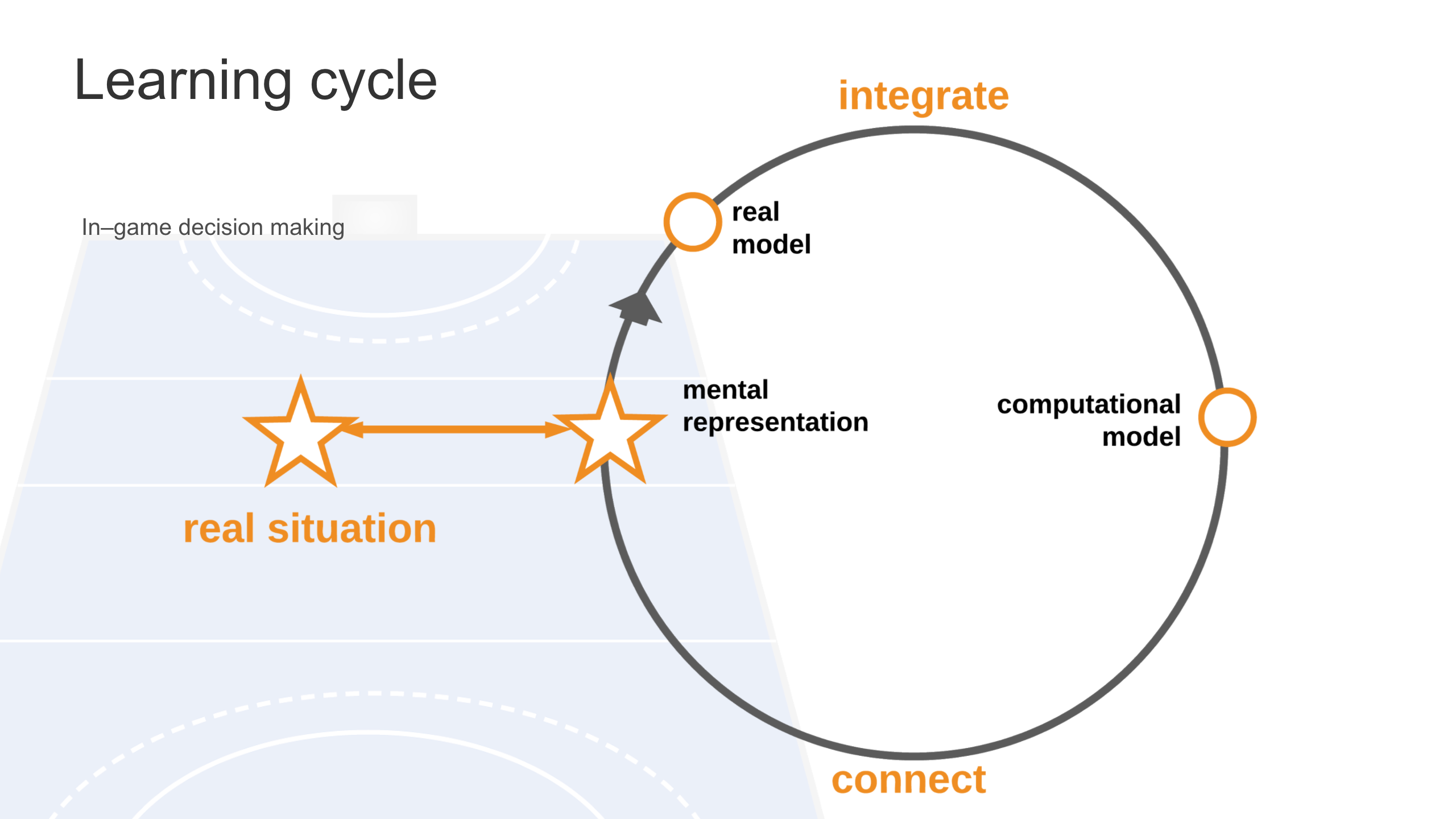
The real situation occurs on the field where a decision is made and an action is executed. Then, the athlete forms a mental representation, processing occurs, and a real model is formed. The real model is integrated into the computational model, which results in a technological feedback, then a connection is made back into game play.

(Butler & Winne, 1995; Cleary & Zimmerman, 2001; Hadwin et al., 2017; Leard & Hadwin, 2001)

Computational modelling and data literacy notes

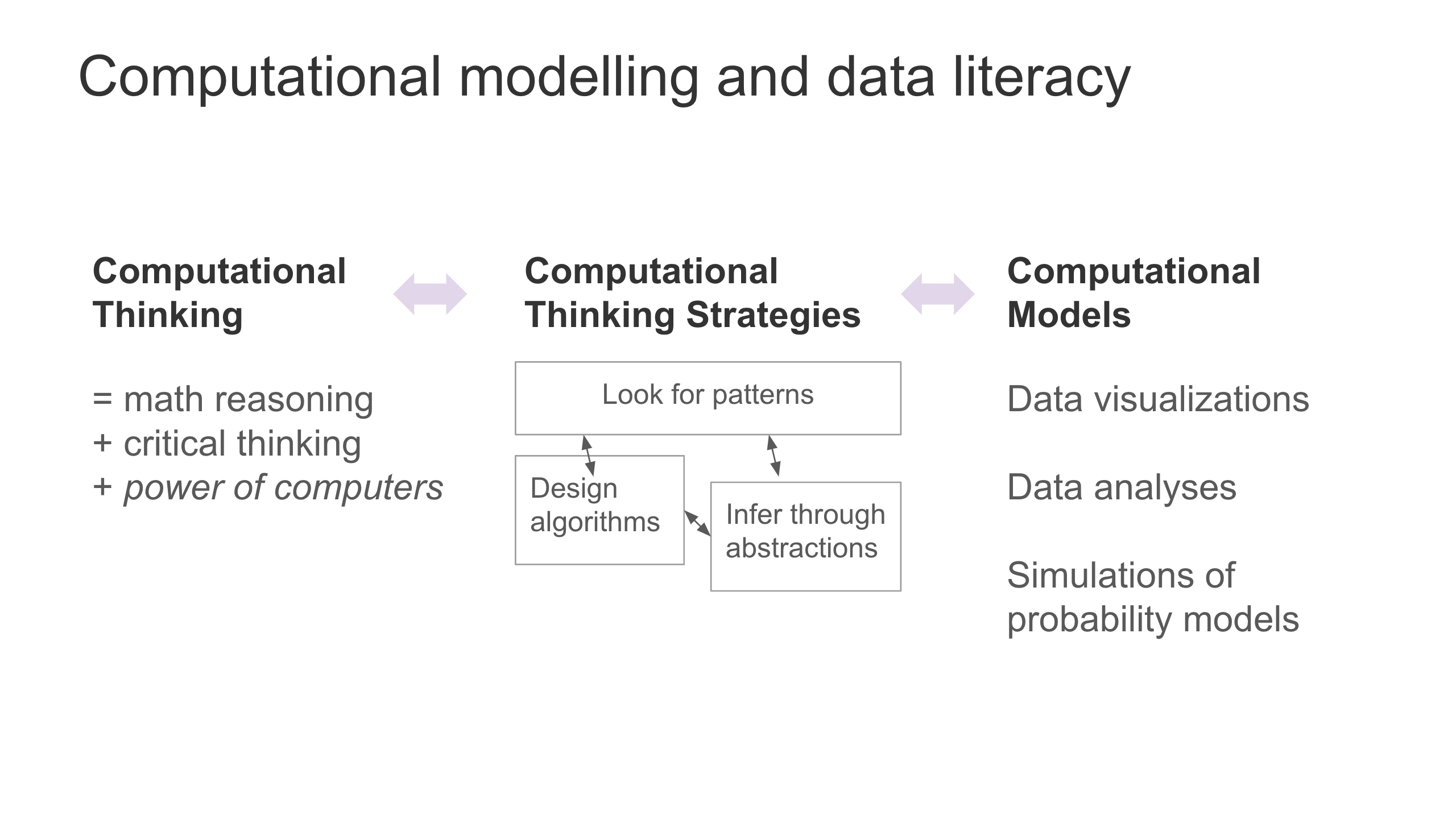
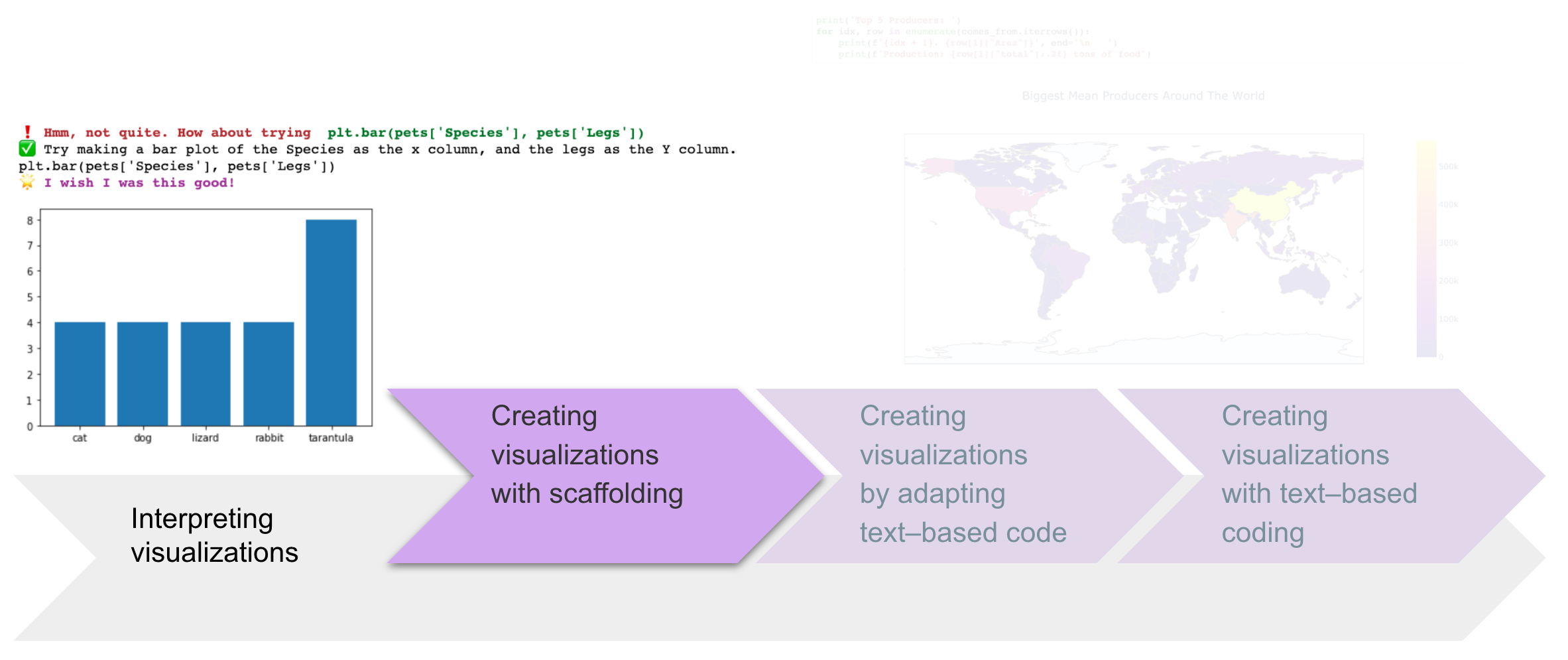
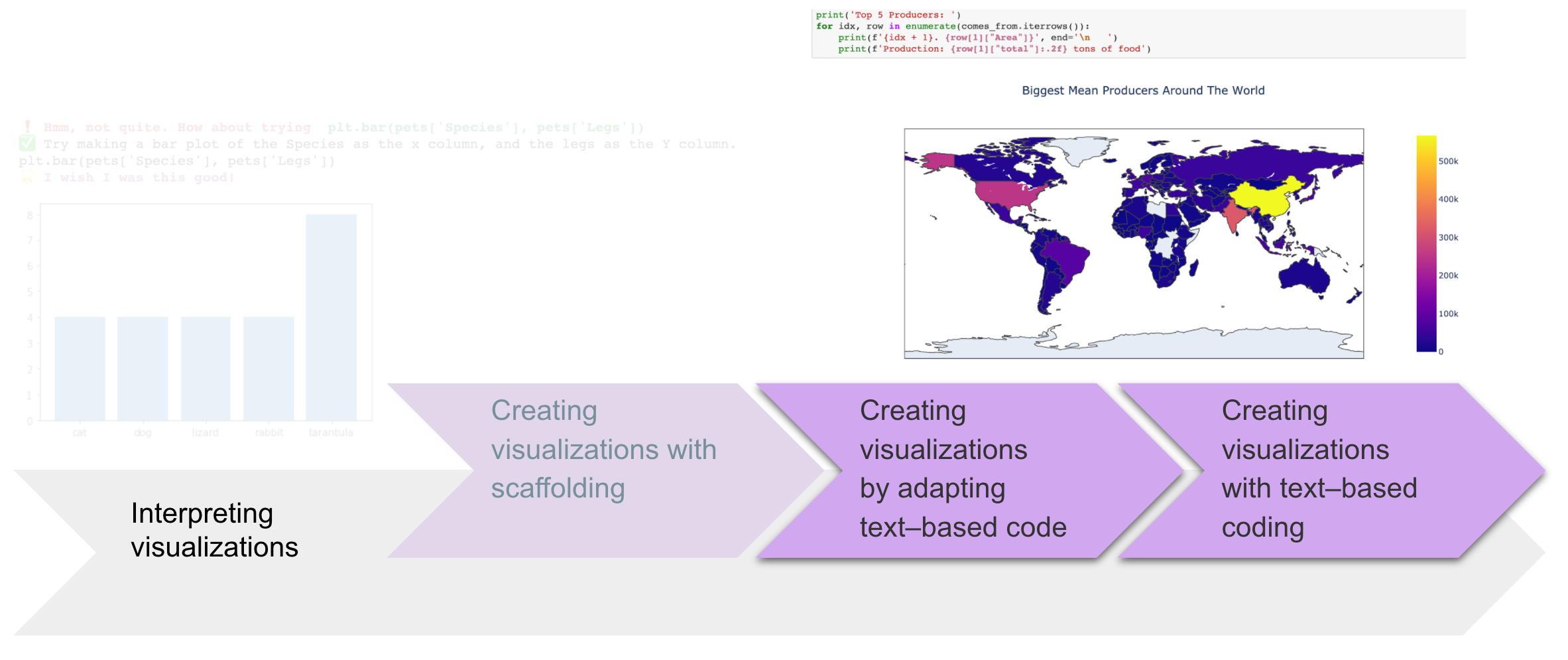
The definition of computational thinking can vary.

Computational thinking within data literacy is math reasoning combined with critical thinking plus the power of computers. We can use computers to do work more efficiently for us, like compute thousands of lines of data.

Under that definition of computational thinking, we can apply computational thinking strategies. The foundational process is decomposing to look for patterns. We can use computer programming to design algorithms to look for patterns. With these algorithms, we can infer through abstractions.

The abstractions can be in the form of computational models: data visualizations (including graphs from the curriculum), data analyses, and simulations of probability models. The data visualizations can extend beyond the curriculum to support math reasoning.

(Berikan & Özdemir, 2019; Gadanidis, 2020; Guadalupe & Gómez-Blancarte, 2019; Leard & Hadwin, 2001)

Data science analysis process notes

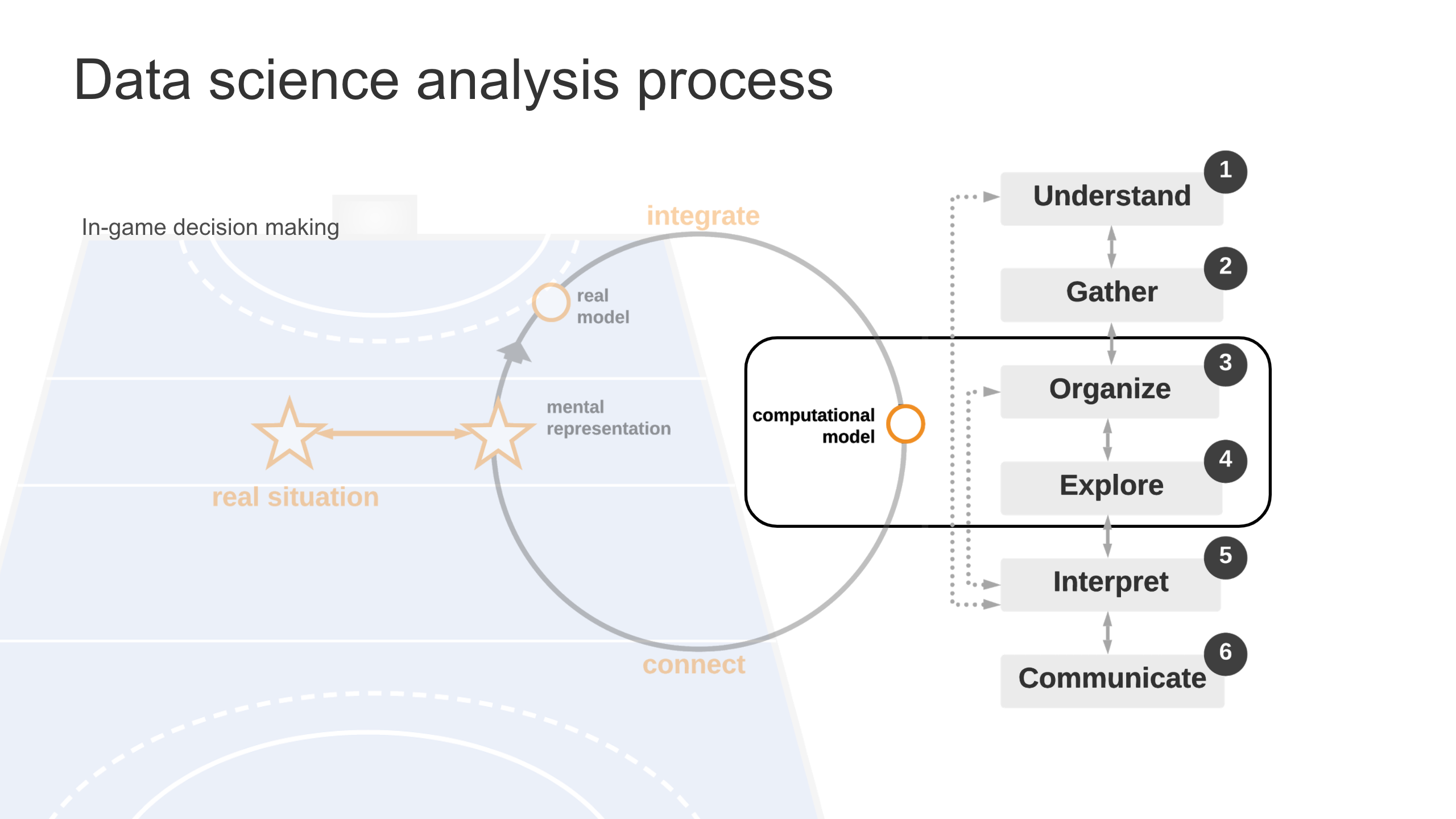
This data science analysis process was modified from how expert data scientists analyze data and aligned to several provincial curricula.

There are six steps:

1. Understand the problem. What questions are we trying to answer?
2. Gather the data. Find the data sources, with the extension of big data sets.
3. Organize the data so we can explore it, usually in the form of a table.
4. Explore the data to create computational models. Usually, there is more than one model. Look for evidence to answer our questions.
5. Interpret the data through inferences. Explain how the evidence answers our questions.
6. Communicate the results. In the context of sports analytics, the communication might be within a team to decide tactical strategies for game play.

(Alberta Education, 2007, updated 2016; Ferri, 2006; Leard & Hadwin, 2001; Manitoba Education and Training, 2020; Ontario Ministry of Education, 2020)

Learning cycle notes

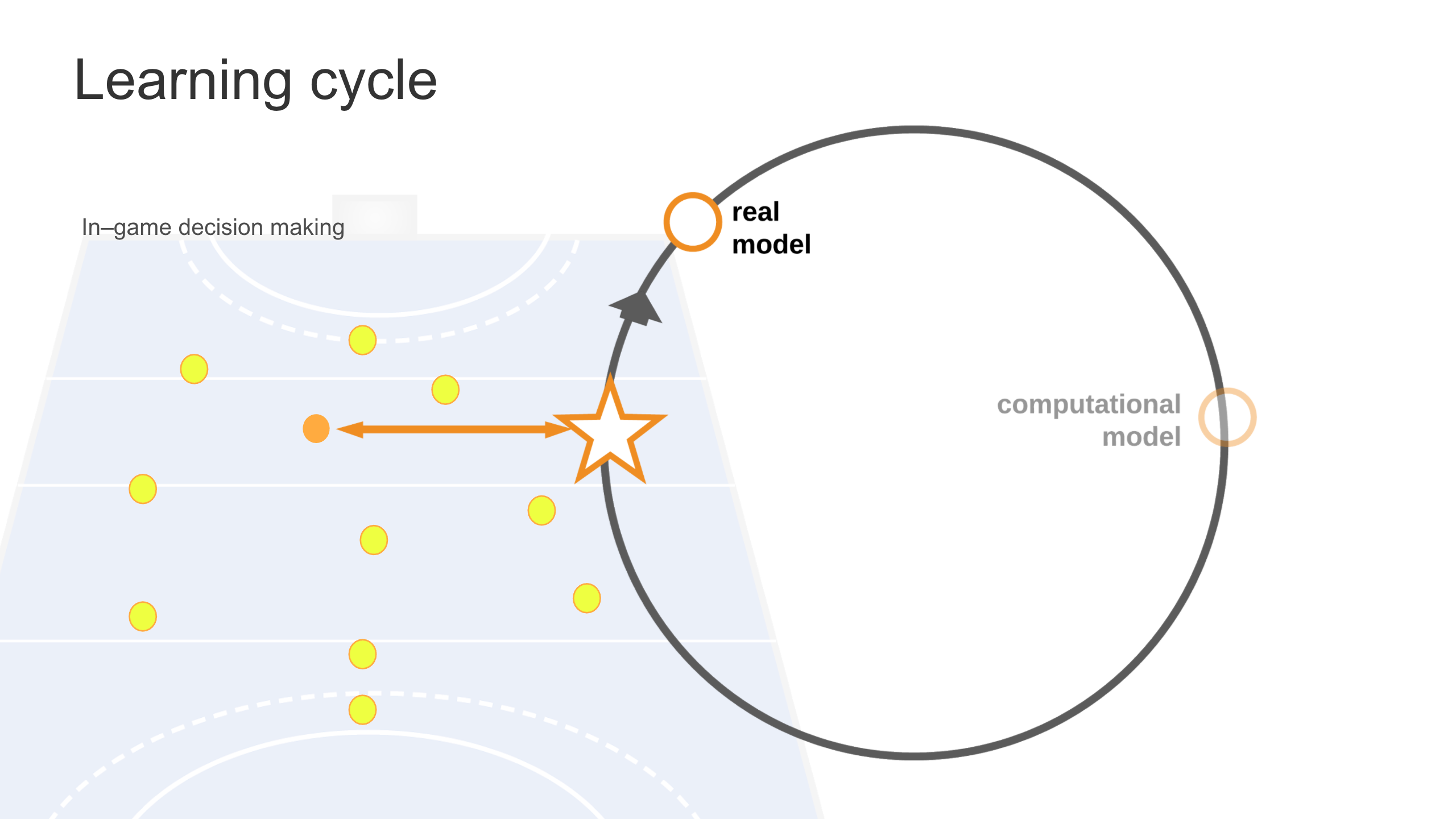
How the individual makes decisions within the collective responsibilities and actions of the team can be considered. In-game decision making involves in-game communication with team members, with each athlete referring to their own real model.

While in-game decision making will always produce a real model, athletes also need to decide when it is appropriate to connect the real model to the computational model and integrate that connection back into game play.

(BC Ministry of Education, 2020; Hadwin et al., 2017; Leard & Hadwin, 2001)

References

Alberta Education. (2000). Physical education [Program of Studies]. https://education.alberta.ca/media/160191/phys2000.pdf

Alberta Education. (2007, updated 2016). Mathematics kindergarten to grade 9 [Program of Studies]. https://education.alberta.ca/media/3115252/2016_k_to_9_math_pos.pdf

Alberta Education. (2017). Career and Ttechnology foundations [Program of Studies]. https://education.alberta.ca/media/3795641/ctf-program-of-studies-jan-4-2019.pdf

BC Ministry of Education. (2020). BC's digital literacy framework. https://www2.gov.bc.ca/assets/gov/education/kindergarten-to-grade-12/teach/teaching-tools/digital-literacy-framework.pdf

Berikan, B., & Özdemir, S. (2019). Investigating “problem-solving with datasets” as an implementation of computational thinking: A literature review. Journal of Educational Computing Research, 58(2), 502–534. https://doi.org/10.1177/0735633119845694

Butler, D. L., & Winne, P. H. (1995). Feedback and self-regulated learning: A theoretical synthesis. Review of Educational Research, 65(3), 245–281. https://doi.org/10.3102/00346543065003245

Cleary, T. J., & Zimmerman, B. J. (2001). Self-regulation differences during athletic practice by experts, non-experts, and novices. I Journal of Applied Sport Psychology, 13(2), 185–206. https://doi.org/10.1080/104132001753149883

Ferri, R. B. (2006). Theoretical and empirical differentiations of phases in the modelling process. ZDM, 38(2), 86–95. https://doi.org/10.1007/bf02655883

Gadanidis, G. (2020, September 2). Shifting from computational thinking to computational modelling in math education [Online plenary talk]. Changing the Culture 2020, Pacific Institute for the Mathematical Sciences.

Guadalupe, T. & Gómez-Blancarte, A. (2019). Assessment of informal and formal inferential reasoning: A critical research review. Statistics Education Research Journal, 18, 8-25. https://www.researchgate.net/publication/335057564_ASSESSMENT_OF_INFORMAL_AND_FORMAL_INFERENTIAL_REASONING_A_CRITICAL_RESEARCH_REVIEW

Hadwin, A., Järvelä, S., & Miller, M. (2017). Self-Regulation, Co-Regulation, and Shared Regulation in Collaborative Learning Environments. Handbook of Self-Regulation of Learning and Performance, 83–106. https://doi.org/10.4324/9781315697048-6

Kastens, K. (2014). Pervasive and Persistent Understandings about Data. Oceans of Data Institute. http://oceansofdata.org/sites/oceansofdata.org/files/pervasive-and-persistent-understandings-01-14.pdf

Leard, T., & Hadwin, A. F. (2001, May). Analyzing logfile data to produce navigation profiles of studying as self-regulated learning [Paper presentaion]. Canadian Society for the Study of Education, Quebec City, Quebec, Canada.

Manitoba Education and Training (2020). Literacy with ICT across the curriculum: A model for 21st century learning from K-12. https://www.edu.gov.mb.ca/k12/tech/lict/index.html

Ontario Ministry of Education. (2020). The Ontario curriculum grades 1‐8: Mathematics [Program of Studies]. https://www.dcp.edu.gov.on.ca/en/curriculum/elementary-mathematics